Τρία από τα πιο παράξενα μαθηματικά παράδοξα

Στα μαθηματικά υπάρχουν πολλά παράδοξα που με πρώτη ματιά φαίνονται αντιφατικά (ή και με δεύτερη και τρίτη ματιά). Ωστόσο αυτά τα παράδοξα μπορούν να εξηγηθούν. Δεν πρόκειται για λάθη, αλλά για υπενθυμίσεις ότι στα μαθηματικά δεν πρέπει να στηριζόμαστε πολύ στη διαίσθησή μας.

Το «Ξενοδοχείο του Χίλμπερτ»

Φανταστείτε ότι φτάνετε σε μια πόλη χωρίς να έχετε κλείσει δωμάτιο σε ξενοδοχείο. Συναντάτε ένα ωραίο ξενοδοχείο, στο οποίο έχει δοθεί το όνομα του διάσημου μαθηματικού Ντέιβιντ Χίλμπερτ. Φτάνοντας στη ρεσεψιόν διαπιστώνετε πως το ξενοδοχείο έχει άπειρα δωμάτια, αριθμημένα με βάση τους φυσικούς αριθμούς: 1, 2, 3, … Ωστόσο, ο ρεσεψιονίστ υποστηρίζει ότι το ξενοδοχείο είναι γεμάτο. Γνωρίζοντας καλά μαθηματικά, του προτείνετε έναν τρόπο να μπορέσει να φιλοξενήσει κι εσάς και οποιονδήποτε άλλον επισκέπτη έρθει. Αρκεί καθένας απ’ όσους ήδη διαμένουν στο ξενοδοχείο να μετακινηθεί στο δωμάτιο που έχει αριθμό κατά 1 μεγαλύτερο από εκείνον του δωματίου όπου διαμένει. Το άτομο που μένει στο δωμάτιο 1 θα πάει στο 2, εκείνο από το 2 θα πάει στο 3 κ.ο.κ. Επειδή το «Ξενοδοχείο του Χίλμπερτ» έχει άπειρο αριθμό δωματίων, ακόμη κι όταν είναι «γεμάτο», συνεχίζει να έχει χώρο για επιπλέον ταξιδιώτες. Αν έρθουν πολλοί μαζί όταν είναι «γεμάτο», οι διαμένοντες θα πρέπει απλώς να μετακινηθούν αρκετά δωμάτια πιο πέρα ο καθένας.

Το πράγμα γίνεται ακόμη πιο παράξενο. Ακόμη κι αν έρθει άπειρος αριθμός επιπλέον ανθρώπων που ζητούν κατάλυμα κι αυτοί μπορούν να φιλοξενηθούν στο πλήρως κατειλημμένο ξενοδοχείο, αρκεί καθένας από τους ήδη διαμένοντες να μετακινηθεί στο δωμάτιο που έχει αριθμό διπλάσιο από αυτό του δωματίου όπου διαμένει έως τώρα, καθώς έτσι θα προκύψουν άπειρα κενά δωμάτια με μονό αριθμό και άπειρα κενά δωμάτια με ζυγό αριθμό. Οι ακολουθίες αριθμών δείχνουν πως ένας άπειρος αριθμός ανθρώπων μπορεί να βρουν δωμάτιο σε ένα ξενοδοχείο με άπειρο αριθμό δωματίων.

Ο Γερμανός μαθηματικός Ντ. Χίλμπερτ παρουσίασε αυτό το υποτιθέμενο παράδοξο σε μια διάλεξή του για την απειρότητα, το 1925. Το παράδειγμα αυτό δείχνει πως δεν μπορούν όλες οι έννοιες να μεταφερθούν από το πεπερασμένο στο άπειρο: Οι δηλώσεις «κάθε δωμάτιο είναι κατειλημμένο» και «το ξενοδοχείο δεν μπορεί να φιλοξενήσει άλλους ανθρώπους» είναι συνώνυμες στον πεπερασμένο κόσμο της καθημερινότητας, αλλά όχι σε έναν κόσμο όπου υπάρχουν απειρότητες.

Το παράδοξο των γενεθλίων

Δεν είναι σπάνιο να είχε διαπιστώσει κανείς τα χρόνια που πήγαινε σχολείο ότι κάποιοι συμμαθητές του τύχαινε να έχουν γενέθλια την ίδια μέρα του έτους. Καταρχάς αυτό μοιάζει με τεράστια σύμπτωση, αφού το έτος έχει 365 μέρες (366 όταν είναι δίσεκτο, αλλά θα το αγνοήσουμε για απλούστευση), ενώ μια τάξη συνήθως έχει γύρω στους 25 μαθητές (και με εγκύκλιο του υπουργείου Παιδείας πια). Η διαίσθησή μας λέει ότι οι πιθανότητες δύο μαθητές να έχουν γεννηθεί την ίδια μέρα του έτους είναι μικρές. Στην πραγματικότητα η πιθανότητα δύο άνθρωποι σε μια ομάδα 23 ατόμων να έχουν κοινά γενέθλια είναι μεγαλύτερη από 50%.

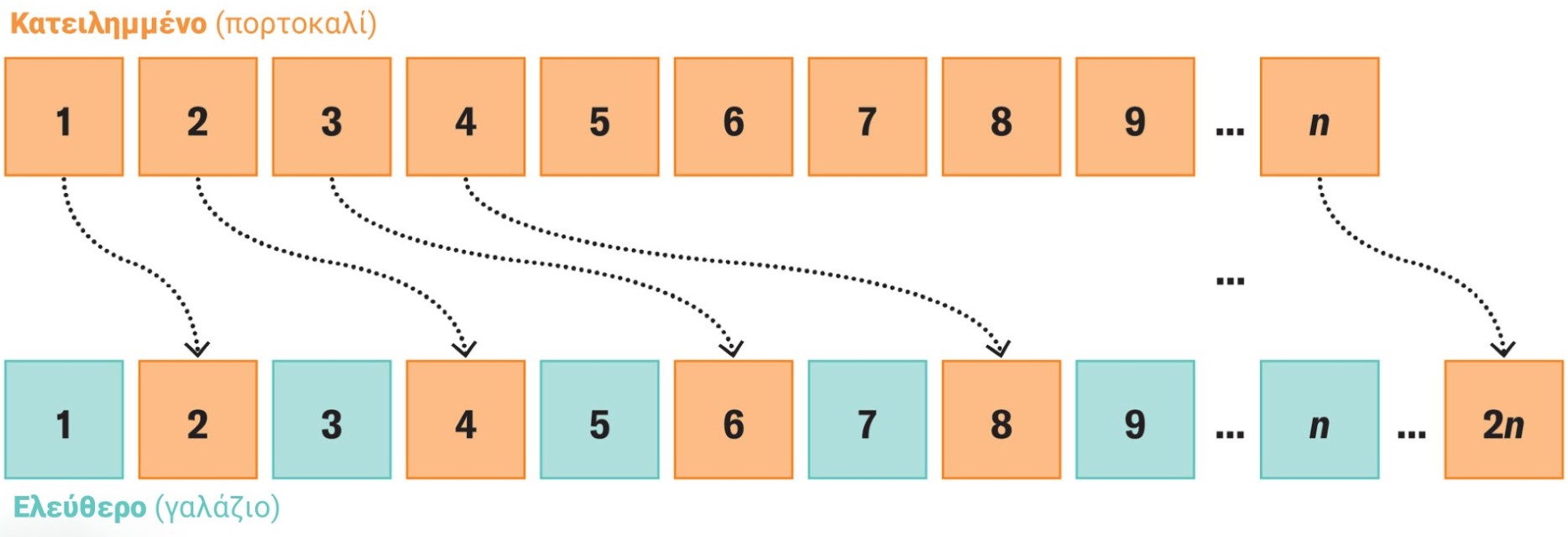
Μετακινώντας κάθε διαμένοντα σε δωμάτιο που έχει αριθμό το διπλάσιο του αριθμού του δωματίου στο οποίο ήδη διαμένει, δημιουργείται χώρος για άπειρο αριθμό επιπλέον ανθρώπων

Για να το καταλάβει καλύτερα κανείς αυτό πρέπει να δει όχι τον αριθμό των ανθρώπων, αλλά τον αριθμό των ζευγών ανθρώπων. Οι 23 μαθητές μπορούν να ομαδοποιηθούν σε (23 x 22) / 2 = 253 ζεύγη και αυτός ο αριθμός ξεπερνάει τον μισό αριθμό ημερών του έτους. Ωστόσο, η πιθανότητα που έχει ένας μαθητής τάξης με 23 παιδιά να έχει γεννηθεί μια συγκεκριμένη μέρα είναι μόλις 1 – ((365 – 1) / 365) ^ 23 = 6,1%. Το παράδοξο των γενεθλίων πηγάζει από το γεγονός ότι από τα ζεύγη μαθητών προκύπτει μεγαλύτερος αριθμός πιθανοτήτων, απ’ ό,τι αν εξετάσει κανείς τους μαθητές μεμονωμένα.

Αυτό είναι κάτι που έχει χειροπιαστή επίπτωση στην κρυπτογραφία. Οταν πρόκειται να υπογραφεί ψηφιακά ένα έγγραφο μετατρέπεται μέσω μιας διαδικασίας σε ακολουθία χαρακτήρων ορισμένου μεγέθους (hash). Αυτή η ακολουθία αλλάζει ακόμη κι αν γίνει η παραμικρή τροποποίηση του κειμένου. Η διαφύλαξη αναλλοίωτης της συγκεκριμένης ακολουθίας σημαίνει πως το έγγραφο δεν πειράχθηκε, καθώς η πιθανότητα να παραχθεί η ίδια ακολουθία από δύο διαφορετικά έγγραφα είναι εξαιρετικά μικρή.

Ωστόσο, κάποιος μπορεί να κάνει «επίθεση γενεθλίων» στη μέθοδο αυτή, δημιουργώντας πολλές διαφορετικές παραλλαγές του εγγράφου προς υπογραφή, από τις οποίες μία σε κάθε ζευγάρι είναι παραλλαγή του κανονικού εγγράφου και μία του τροποποιημένου, συγκρίνοντας τις παραγόμενες ακολουθίες κατά ζεύγη. Ετσι μπορεί να βρει πιο γρήγορα δύο έγγραφα που οι «υπογραφές» τους θα είναι ίδιες, αντί να προσπαθήσει να φτιάξει ένα έγγραφο που έχει ίδια ακολουθία – υπογραφή με το έγγραφο που θέλει να αλλοιώσει. Τότε δίνει για ψηφιακή υπογραφή το έγγραφο με το κανονικό περιεχόμενο, αλλά μετά ισχυρίζεται πως υπογράφηκε από το θύμα το τροποποιημένο έγγραφο, καθώς είναι αδύνατο να ανιχνευτεί η απάτη.

Η «Αντινομία του Ράσελ»

Ο Βρετανός φιλόσοφος Μπέρτραντ Ράσελ διατύπωσε ένα παράδοξο το 1901, που ονομάστηκε «Αντινομία του Ράσελ», καθώς περιγράφει δύο φαινομενικά αντικρουόμενες ιδέες. Σε αντίθεση με τα προηγούμενα δύο παράδοξα, η «Αντινομία του Ράσελ» δεν είναι απλώς κάτι που ξεγελά τη διαίσθησή μας. Αντιβαίνει στους κανόνες της λογικής αυτούς καθαυτούς. Η αντινομία παράγει δηλώσεις που δεν μπορεί να είναι ούτε αληθείς ούτε ψευδείς.

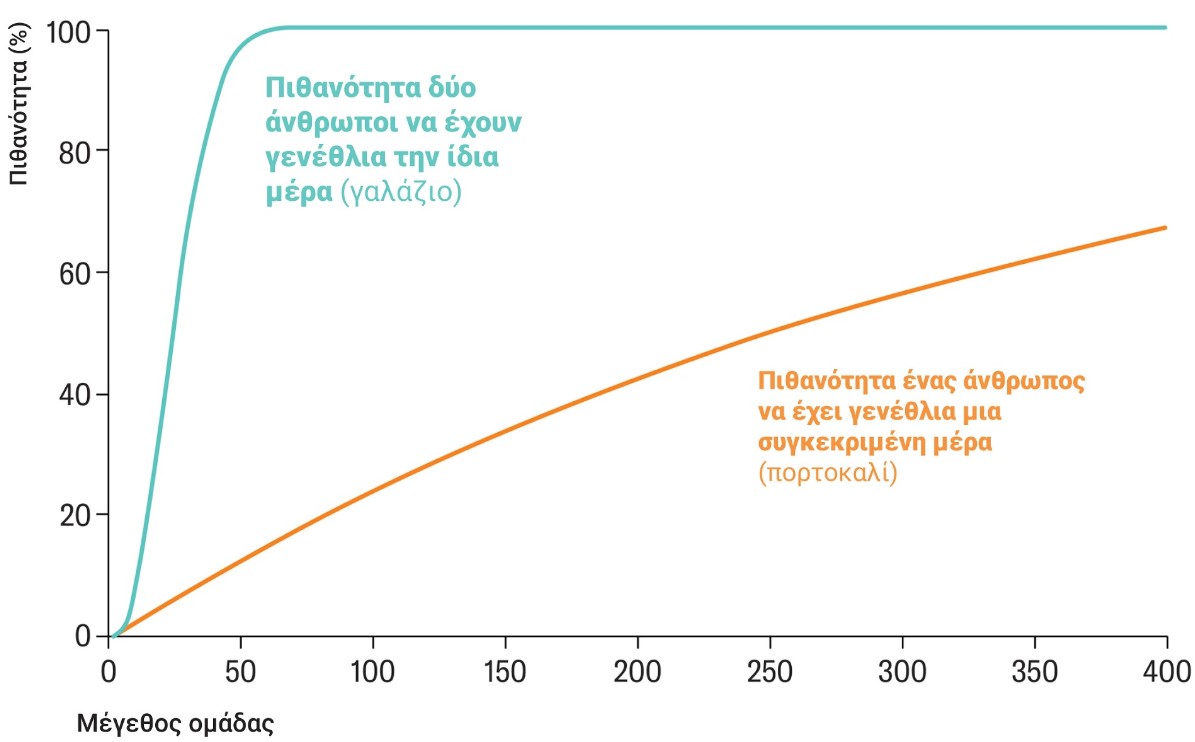
Η γαλάζια γραμμή δείχνει την πιθανότητα δύο άνθρωποι που ανήκουν σε μια ομάδα ανθρώπων να έχουν γενέθλια την ίδια ημερομηνία (το μέγεθος της ομάδας στον οριζόντιο άξονα). Η πορτοκαλί γραμμή αντιστοιχεί στην πιθανότητα ένας άνθρωπος να έχει γενέθλια μια συγκεκριμένη ημερομηνία

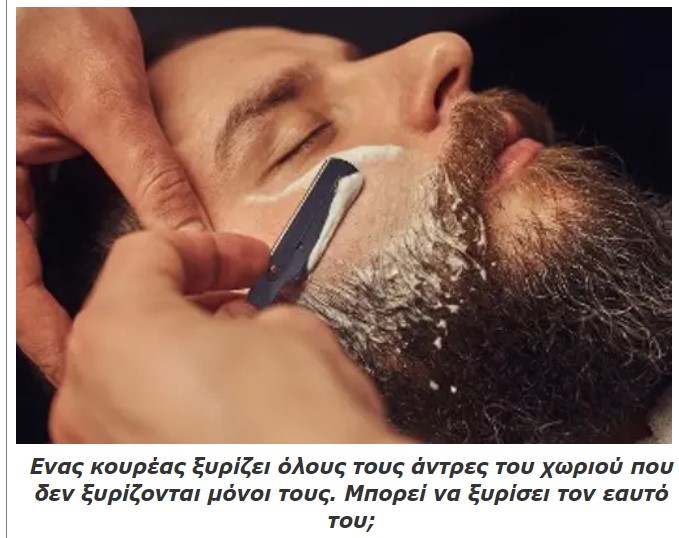
Μια από τις πιο γνωστές παραλλαγές της είναι το «παράδοξο του κουρέα». Ας υποθέσουμε ότι ένας κουρέας ξυρίζει όλους τους άντρες στο χωριό του, που δεν ξυρίζονται μόνοι τους και μόνο αυτούς. Αραγε ο ίδιος ο κουρέας ξυρίζει τον εαυτό του; Αν το κάνει, τότε δεν ανήκει στην ομάδα των ανθρώπων που δεν ξυρίζονται μόνοι τους. Αλλά αν δεν ξυρίζει τον εαυτό του, τότε εξ ορισμού θα έπρεπε να τον ξυρίζει, αφού όλοι οι άντρες κάτοικοι που δεν ξυρίζονται μόνοι τους πηγαίνουν σ’ αυτόν.

Το παράδοξο βασίζεται σε ασαφή προσδιορισμό συνόλων. Την εποχή που ο Ράσελ παρουσίασε την αντινομία του, ένα σύνολο στα μαθηματικά αντιστοιχούσε σε μια συλλογή πραγμάτων. Οι φυσικοί αριθμοί, για παράδειγμα, σχηματίζουν ένα σύνολο, όπως και η ομάδα των αντρών κατοίκων που δεν ξυρίζονται μόνοι τους. Αυτός ο ορισμός, όμως, επιτρέπει στα σύνολα να περιέχουν τον εαυτό τους, ή να αναφέρονται στον εαυτό τους ως ενιαίο αντικείμενο και αυτές οι ιδιότητες οδηγούν σε αντιφάσεις. Η αντινομία του Ράσελ οδήγησε στο τέλος αυτού που οι μαθηματικοί αποκάλεσαν «απλοϊκή θεωρία συνόλων».

Τα θεμέλια των μαθηματικών συνεχίζουν να στηρίζονται στη θεωρία συνόλων. Αλλά τα σύνολα δεν είναι πια απλές συλλογές. Πρέπει να πληρούν συγκεκριμένες συνθήκες, όπως να συντίθενται από ήδη υπάρχοντα σύνολα και να μην αναφέρονται στον εαυτό τους. Αυτές οι συνθήκες αποκλείουν αντινομίες όπως το παράδοξο του κουρέα. Με πιο μαθηματική διατύπωση, οι άνθρωποι του χωριού που βγάζουν γένια και είναι άντρες σχηματίζουν ένα σύνολο Α. Αυτό το σύνολο περιλαμβάνει τους άντρες που ξυρίζονται μόνοι τους και εκείνους που πηγαίνουν στον κουρέα. Το σύνολο Β αποτελεί τους πελάτες του κουρέα. Για να σχηματιστεί ακολουθούνται οι κανόνες της μοντέρνας θεωρίας συνόλων: Αν ο κουρέας είναι άντρας με μούσι, δηλαδή μέλος του συνόλου Α, τότε το σύνολο των πελατών του δεν μπορεί να οριστεί ως «όλοι οι άντρες κάτοικοι που δεν ξυρίζονται μόνοι τους», καθώς σε αυτήν την περίπτωση ο ορισμός θα αναφερόταν στον εαυτό του, αφού τόσο ο κουρέας, όσο και οι πελάτες του θα ήταν μέλη του συνόλου Α. Η σύγχρονη θεωρία συνόλων απλώς δεν επιτρέπει έναν τέτοιο ορισμό. Αλλά αν ο κουρέας δεν είναι μέλος του συνόλου Μ, αν για παράδειγμα είναι γυναίκα, ή άντρας σπανός, τότε ο ορισμός επιτρέπεται.

Αν και όλα τα γνωστά μαθηματικά παράδοξα επιλύονται, δεν υπάρχει κάποια εγγύηση ότι δεν θα προκύψει ποτέ ένα άλυτο παράδοξο με βάση τους κανόνες των μαθηματικών. Ο Κουρτ Γκέντελ το απέδειξε ήδη από τη δεκαετία του 1930. Προς το παρόν ας παραμείνουμε με την ανακούφιση των εξηγήσεων για τα γνωστά παράδοξα.